Потери тепла с уносом

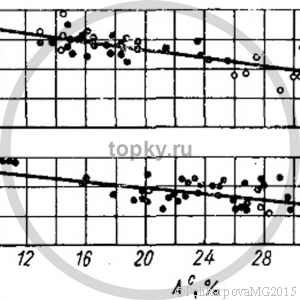
Потери тепла с уносом

Основными факторами, влияющими на потери тепла с уносом q_4ун в слоевых топках, являются: дутьевая форсировка слоя, содержание пылевых частиц в угле и выход летуцих топлива.

Широко распространено мнение, что для топок с забрасывателями, если только осуществляется непрерывный, а не кучный заброс топлива, значения q_4ун должны быть повышенными, поскольку мелкие частицы беспрепятственно отсеиваются при забросе. В известной мере это, конечно, имеет основание, но практически потери с уносом и для других слоевых топочных устройств составляют не меньшие величины, хотя все топливо и укладывается толстым слоем на решетку, в котором «костяк» из крупных частиц может удерживать мелкие частицы.

Важную роль в отношении уноса играет степень равномерности горения слоя по длине решетки. В топках с механическими забрасывателями она наиболее велика, вследствие чего неблагоприятный фактор - свободное отвеивание частиц топлива при забросе - в значительной мере компенсируется благоприятным фактором - меньшими скоростями газов под слоем. Если же взять для сравнения топки с обычной цепной решеткой или с шурующей планкой, то в них горение слоя происходит в основном на протяжении двух средних дутьевых зон, что предопределяет резкую неравномерность газового потока. Часто имеет место также образование кратеров в слое. При шурующей планке, помимо всего прочего, неблагоприятно сказывается ворошение слоя на решетке. Как ни странно, унос достаточно большой и в топках с нижней подачей.

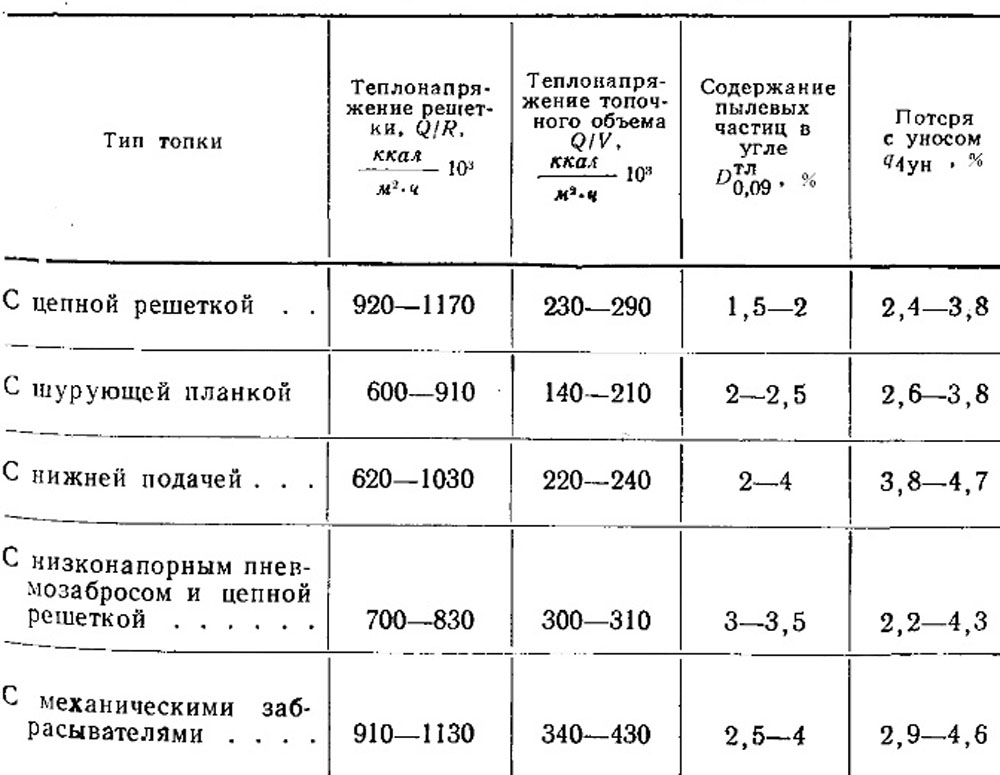
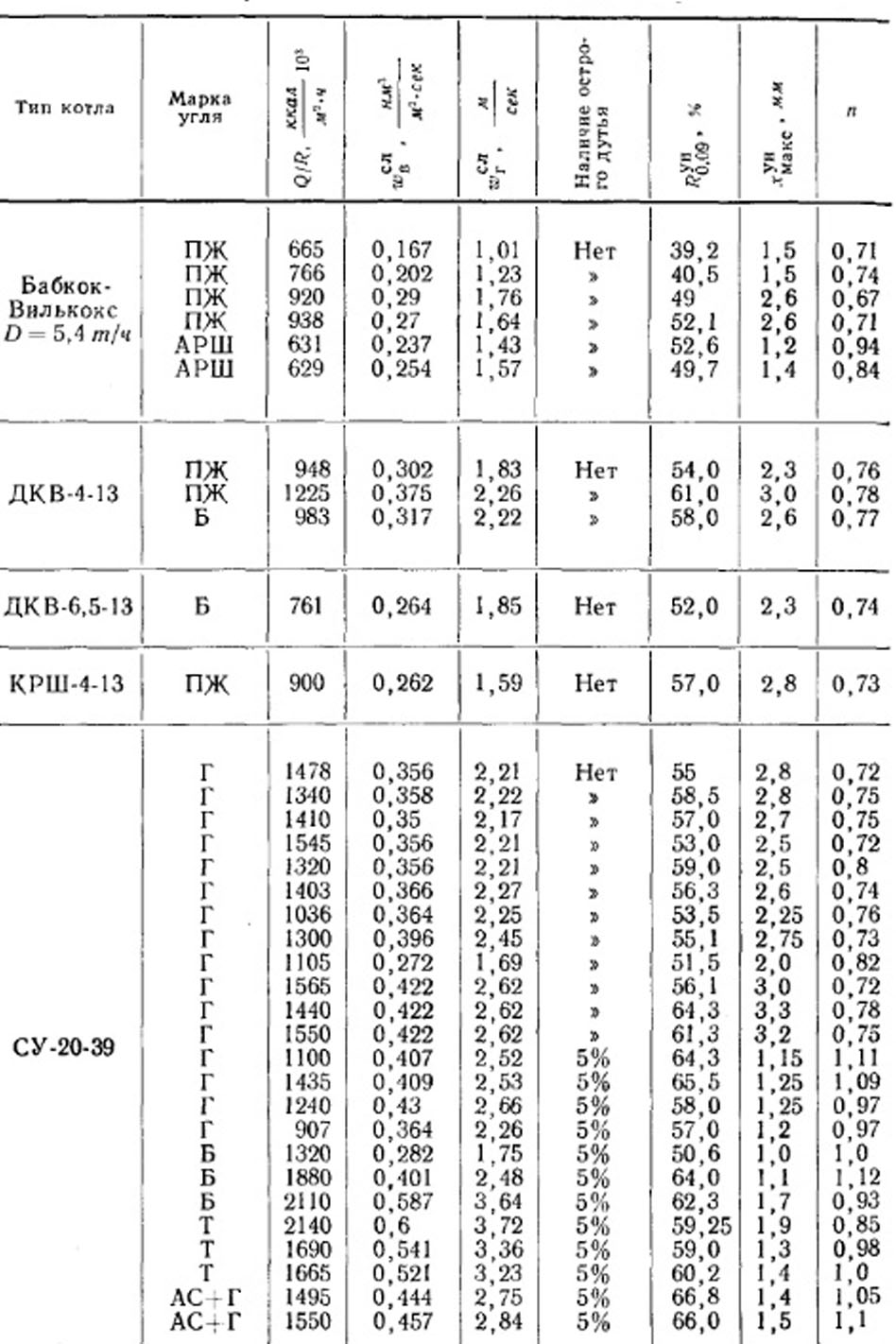
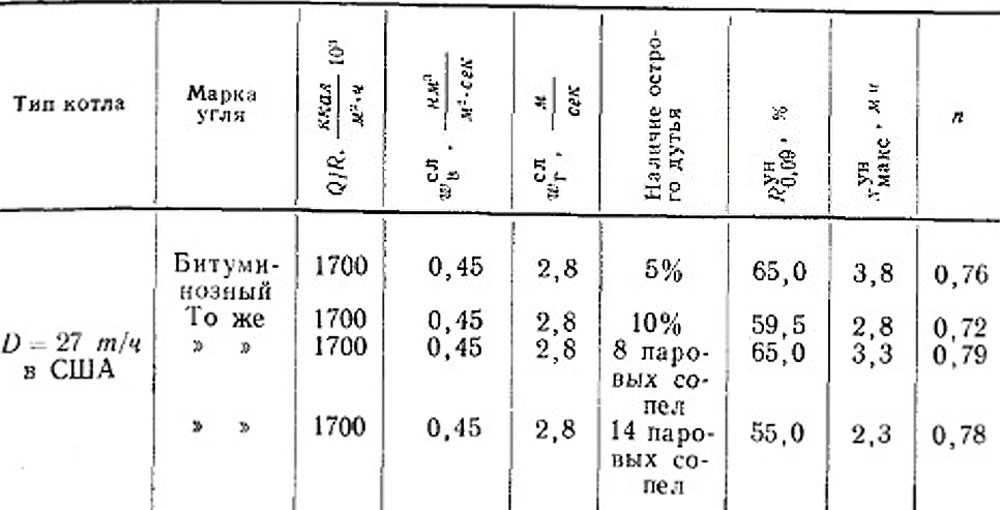
Для иллюстрации в табл. 8-2 приведены значения потерь с уносом для топок с цепной решеткой, с шурующей планкой, с нижней подачей и с забрасывателями, причем подобраны опыты, проведенные при близких теплонапряжениях решетки и содержаниях пылевых частиц в угле.

Таблица 8-2. Потери тепла с уносом для разных слоевых механических топок (при сжигании каменных углей марок Г, Д, ПЖ)

Многие полагают, что потери тепла с уносом должна резко возрастать с увеличением теплонапряжения решетки. Обычно это возрастание принимается по квадратичному закону согласно формуле Л. К. Рамзина, рекомендуемой ВТИ для тепловых расчетов котельных агрегатов:

где α - некоторый опытный коэффициент, отражающий характеристики и гранулометрический состав топлива, размеры и конфигурацию топочной камеры, режим топки и др.

На самом деле такая зависимость не является справедливой для слоевых топок в тех диапазонах тепловых нагрузок, в которых они работают. Потери с уносом мало изменяются с повышением теплонапряжения решетки.

Теоретически возможность потери тепла с уносом из топки частиц топлива того или иного размера при их сферической форме определяется неравенством:

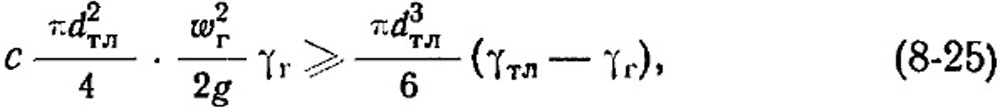
Где ω_г - скорость газового потока м/сек; d_тл - диаметр частицы топлива, м; γ_тл- кажущийся удельный вес топлива, кг/м³; γ_г - удельный вес газов, кг/м³; g - ускорение силы тяжести, м/сек²; с - коэффициент сопротивления при внешнем обтекании, зависящий от критерия Рейнольдса,

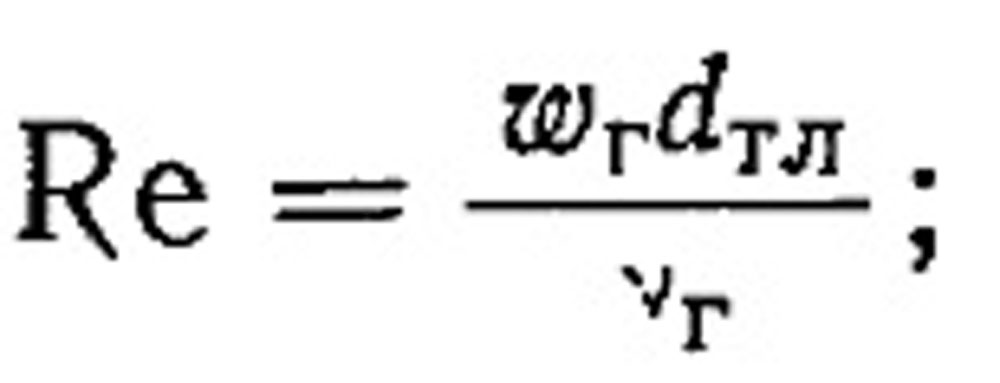
здесь v_г — кинематическая вязкость газов, м²/сек.

Левая часть уравнения (8-25) представляет собой подъемную силу, создаваемую потоком газов по отношению к частице, а правая часть - вес частицы с поправкой на вытесняемый объем газов (по закону Архимеда).

Максимальный диаметр уносимых частиц в зависимости от скорости газового потока будет равен:

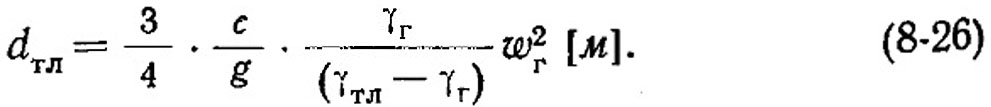
Выражение

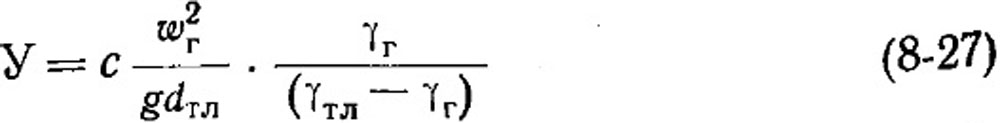
Получило название критерия уноса. Для частиц сферической формы он равен 4/3=1,33. Значения этого критерия резко снижаются в случае частиц неправильной формы, обладающих большой парусностью.

В области Re=1000÷200000 коэффициент с постоянен и равен 0,48. При этом справедлив квадратичный закон изменения dтл  от wr, что и положено в основу формулы (8-24).

В действительности для топок с механическими забрасывателями и ряда других слоевых топочных устройств характерна область Re=l,5÷10, где коэффициент с значительно изменяется. Здесь формула (8-26) не может быть непосредственно использована из-за отсутствия простой математической связи между с и Re.

Чтобы обойти это затруднение, воспользуемся рис. 8-17, на котором дана зависимость ω_г от d_тл через критерии Слихтера S и Кирпичева Ki (при значении критерия уноса У=4/3):

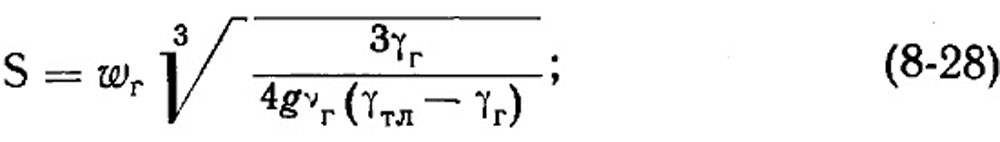
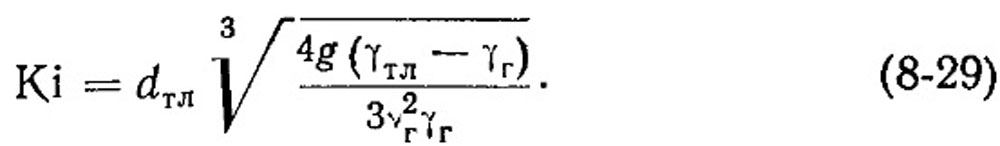
Изучение указанной зависимости показало, что она практически линейна в области S=0,32÷3, Ki=3÷15, соответствующей условиям работы слоевых топок, и может быть определена уравнением

Отсюда легко вывести формулу, непосредственно связывающую диаметр частицы и скорость газов:

подставим значения S и Ki

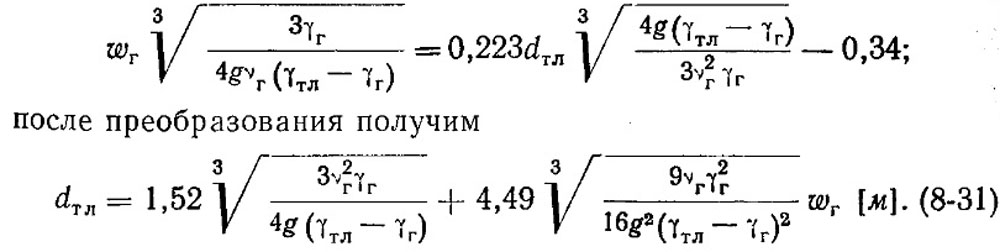
Можно видеть, что зависимость d_тл от ω_г для слоевых топок является теоретически линейной, а не квадратичной.

Как показывают результаты испытаний, количество уноса для полностью открытых топок с механическими забрасывателями определяется в основном скоростью газов над слоем ω_г^сл(или дутьевой форсировкой слоя до ω_в^сл).

Для вычисления wгсл примем следующие упрощенные формулы:

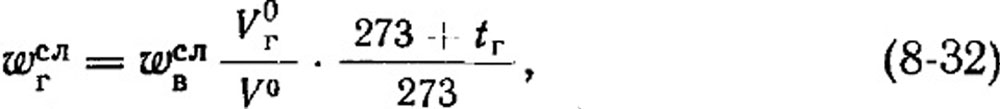
или подставив значение w_г^сл согласно выражению (8-11)

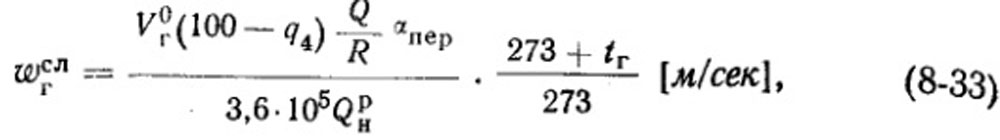
где V_г - теоретическое количество продуктов полного сгорания на 1 кг топлива, нм³/кг; V⁰ - теоретическое количество воздуха, необходимое для полного сгорания топлива, нм3/кг; температура газов над слоем, °С; q₄ - потеря от механического недожога, %; Q/R - теплонапряжение решетки, ккал/ (м³Xч); α_пер - коэффициент избытка первичного воздуха; Q^р_н - теплота сгорания топлива рабочая низшая, ккал/кг.

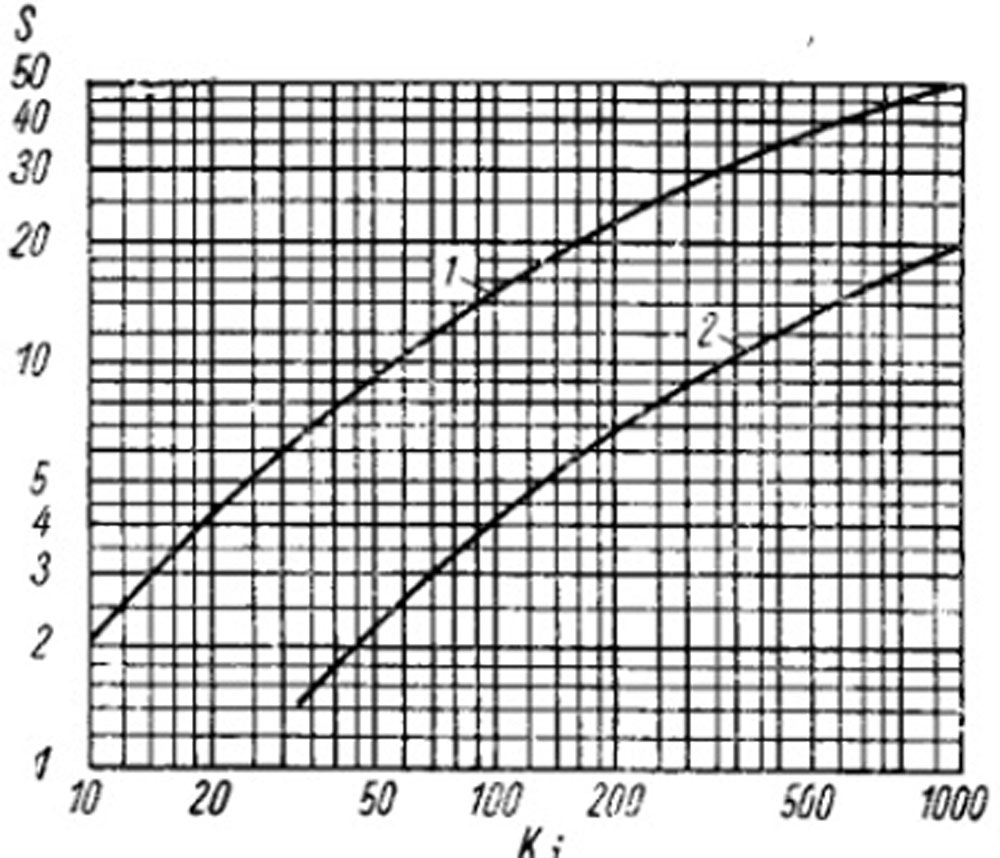
Рис. 8-17. Зависимость критерия Слихтера от критерия Кирпичева. 1 - при. У=4/3; 2 - при. У=0,14.

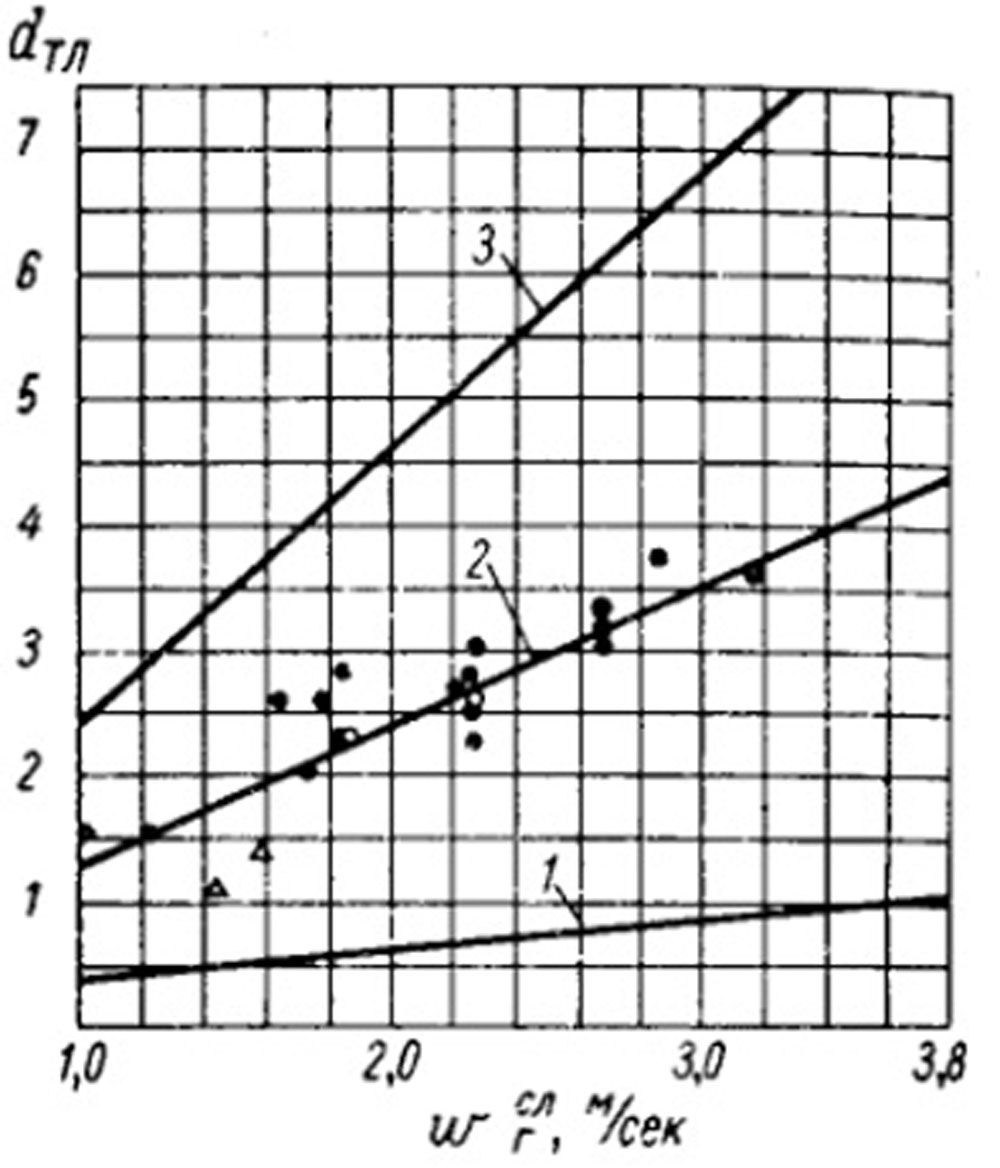
Рис. 8-18. Максимальный размер частиц уноса из топок с механическими забрасывателями в зависимости от скорости газов над слоем. 1 - теоретическая зависимость при У - 4/3; 2 - фактическая зависимость; 3 - условие кипения при У=0,4. а)  • - каменный уголь;  б) ο - бурый уголь; в) Δ - антрацит.

На рис. 8-18 показана теоретическая зависимость d_тл от w^л_г (прямая 1) для условий, которые обычно имеют место в топках с забрасывателями: Q/R= 400÷1800 тыс. ккал/(м²Xч); α_пер=1,32÷0,9; t_г - 1300°С; γ_г=0,226 кг/м3; v_г=245X10^-6 м²/сек; ω^сл_в =0,16÷0,47 нм³/(м²Xсек); w^cлг =1,01÷2,97 м/сек; w^сл_г/w^сл_в= 6,32; γ_тл=765 кг/м³ (без влаги и летучих); S=0,46÷1,35 и Ki=3,6÷7,6 (характеристики, связанные с топливом, заданы для донецкого угля марки Д).

Прямая 1 на рис. 8-18 определяется уравнением:

причем расчетный размер частиц меняется в пределах d_тл=0,4÷0,84 мм.

На график нанесены опытные точки, полученные на основе рассевов проб уноса, отобранных при испытаниях разных топок с механическими забрасывателями. Можно видеть, что они легли намного выше теоретической прямой. Фактические размеры частиц оказываются в 3 - 4 раза больше расчетных. Опытным точкам соответствует прямая 2 при скоростях газов приблизительно в 5 раз больших по сравнению со средними скоростями газов над слоем w^сл_г. Прямая 2 может быть выражена уравнением:

Расхождение между теоретическим расчетом и опытными данными в отношении размеров частиц, уносимых газовым потоком, давно известно. Его объясняют разными причинами: местными повышенными скоростями газов, фонтанирующим действием воздуха, прорывающегося через отдельные кратеры в слое, наличием газовой оболочки вокруг частиц, влиянием фактора формы частиц и др.

Опытами Е. С. Льва установлено, что при начале нарушения устойчивости слоя (начале кипения) критерий уноса У, отнесенный к скорости газов в просвете слоя, не зависит от формы частиц и равен 0,14. На рис. 8-17 кривая 2 устанавливает связь между критериями S и Ki при указанном значении критерия У.

Для тонкого горящего слоя, который имеет место в топках с механическими забрасывателями, можно задать просвет слоя равным 0,5. Тогда скорость газов в просвете слоя составит w^п_г =2 w^сл_г. Соответственно получим прямую 3 на рис. 8-18, позволяющую определять размеры частиц, находящихся в состоянии кипения над слоем. Как видно, данная прямая прошла намного выше опытных точек для уноса. В пределах w^сл_г=1,01÷2,97 м/сек, w^ст₁=2,02÷5,94 м/сек размер частиц составляет d_тл=2,38÷6,75 мм.

Если принять У=0,14, но отнести данный критерий к средней скорости газов над слоем w^сл_г, то получим зависимость, почти совпадающую с прямой 2 на рис. 8-18, которая хорошо проходит через опытные точки. Возможно, что результаты опытов Льва справедливы и для случаев отвеивания частиц топлива из слоя. Это требует, конечно, дополнительной проверки.

Поскольку уравнение (8-35) удовлетворяет опытным данным, то примем его за основу в дальнейших расчетах возможного количества уноса. Для практических целей удобнее связать d_тл с w^сл_г. При w^сл_г /w^сл_в= 6,32, что было задано раньше, получим:

Соответствующая прямая с опытными точками показана на рис. 8-19, а.

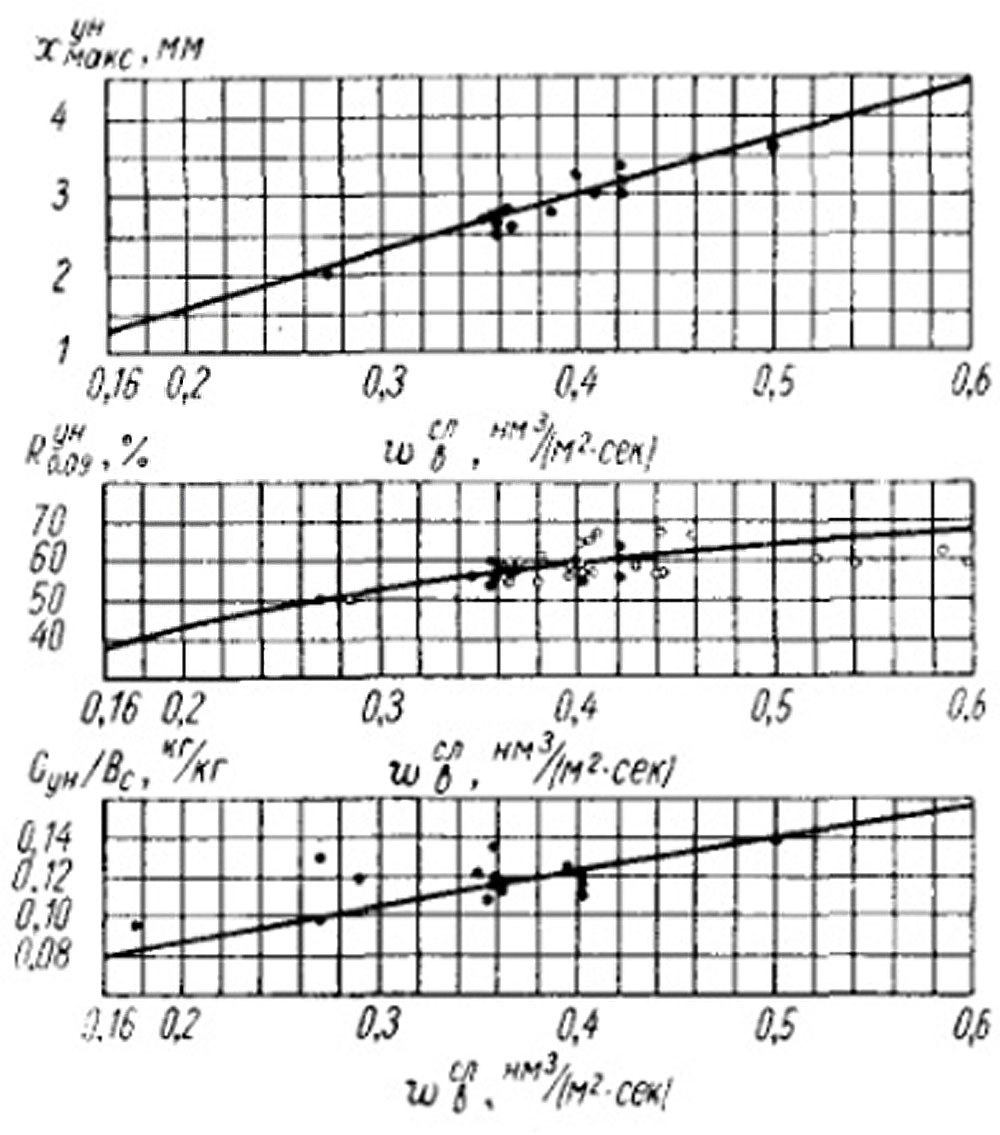
Рис. 8-19. Крупность уноса и его количество в зависимости от дутьевой форсировки слоя: а - максимальный размер частиц; б - полный остаток на сите 0,09 мм; в - количество уноса на 1 кг сухого топлива. • - без острого дутья; ο - с острым дутьем.

Максимальный размер частиц уноса не определяет еще непосредственно количество уноса, так как по условиям сепарации не все частицы данного размера могут улететь с газовым потоком. Рассматривая топку как чистый сепаратор, в котором происходит отделение мелких частиц от остальной массы топлива, возможно составить следующее уравнение баланса частиц размером 0 - 0,09 мм:

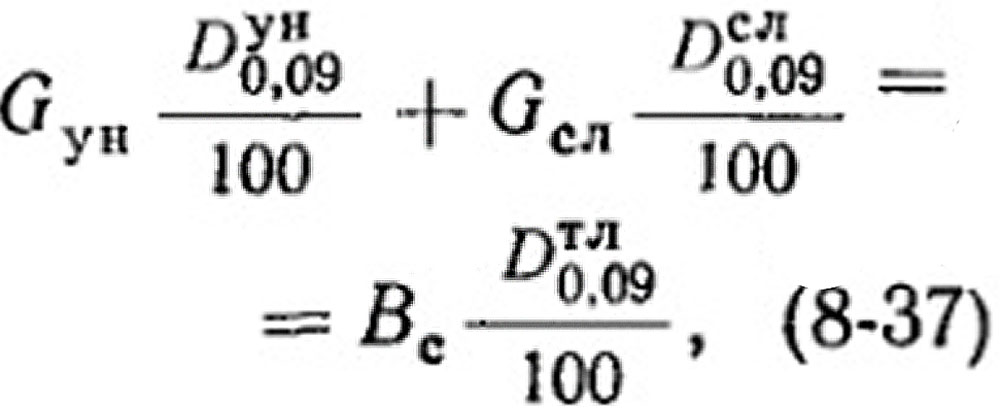
где В_с - количество сухого топлива, подаваемого в топку, кг/ч; G_ун - количество уноса из топки, кг/ч; G_сл- количество топлива, остающегося в топке (в слое),кг/ч; D^тл_0,09 - содержание частиц 0 - 0,09 мм в топливе, уносе и слое, %.

Подставив G_сл=В_с-G_yн и произведя преобразования, получим:

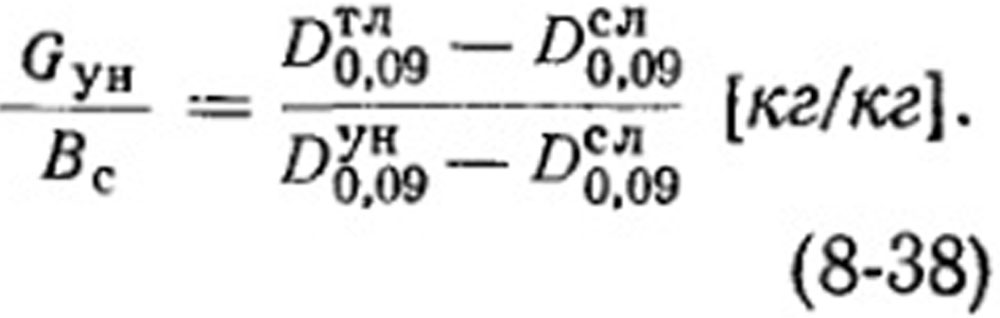
Предположим, что D^сл_0,09=0, т. е. все частицы менее данного размера полностью отвеиваются и переходят в унос. Тогда

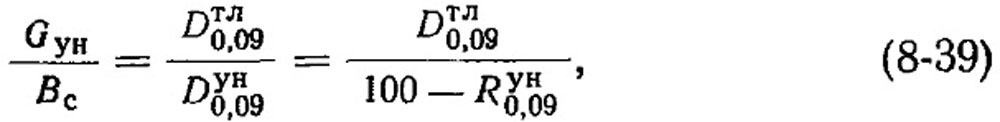
Где R^ун_0,09 - полный остаток на сите 0,09 мм для уноса, %.

Для установления связи между полным остатком на сите и максимальным размером частиц воспользуемся формулой, вытекающей из зависимости (1-1):

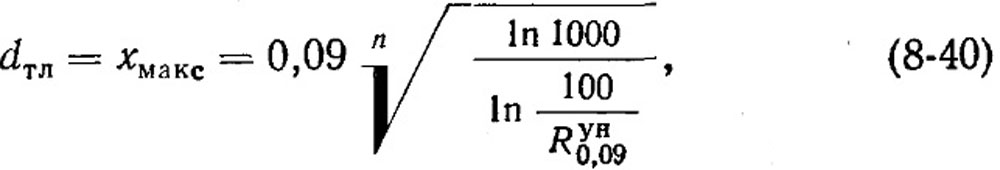
где х_макс - максимальный размер частиц, мм; n - показатель равномерности.

Так как эта формула сложна для вычислений, то удобнее пользоваться вместо нее рис. 8-20.

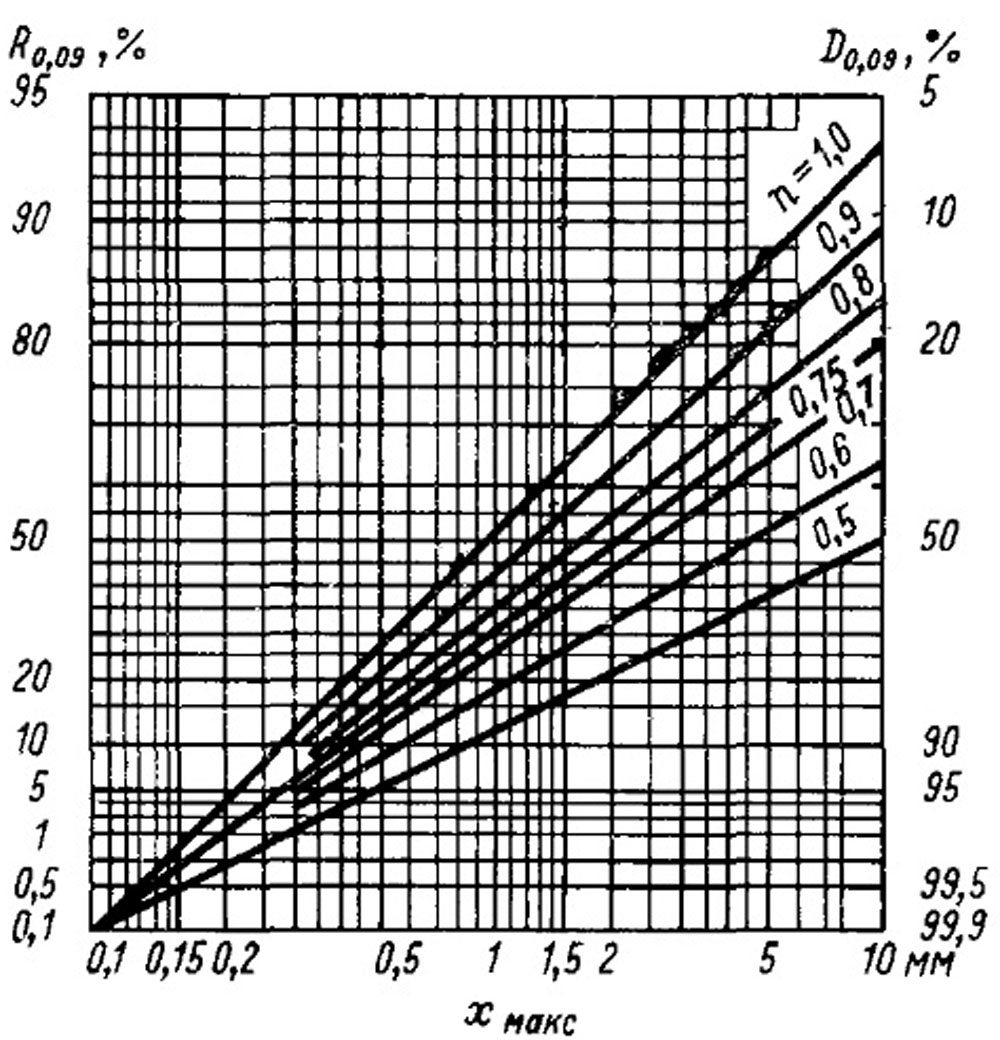
Рис. 8-20. Полный остаток на сите в зависимости от максимального размера частиц.

Значения показателя равномерности п при отсутствии острого дутья обычно близки к 0,75, что видно из табл. 8-3, где приведены некоторые данные по зерновому составу уноса.

Таблица 8-3. Зерновой состав уноса из топок с механическими забрасывателями.

На рис 8-19 показана зависимость R^ун_0,09 при n=0,75. Как видно, опытные точки хорошо совпадают с расчетной кривой. Исходя из рис. 8-19, б можно легко построить зависимость G_yн/B_c от при заданной величине D^сл_0,09 .Если принять D^сл_0,09 =5%, что характерно для многих современных сильно заштыбленных рядовых углей, то получим рис.8-19, а. Зависимость практически линейна и подчиняется уравнению:

На рис. 8-19,6 нанесены опытные точки, причем можно видеть, что они удовлетворительно легли около расчетной прямой.

Если принять значение w^сл_в согласно формуле (8-12), то уравнение (8-41) примет вид:

Подсчеты по последнему уравнению показывают, что при изменении теплонапряжения решетки в пределах от 400 до 1800 тыс. ккал/(м²Xч) - в 4,5 раза, количество уноса увеличивается всего в 1,8 раза, т. е. незначительно (соответственно должна возрастать и потеря тепла с уносом при постоянном содержании горючих в уносе).

Зная величину G_yн/B_c и задавшись содержанием горючих в уносе Г_ун, можно подсчитать значение потери с уносом по формуле

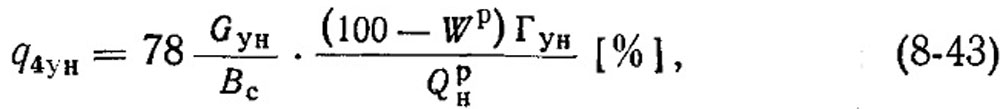
или приближенно

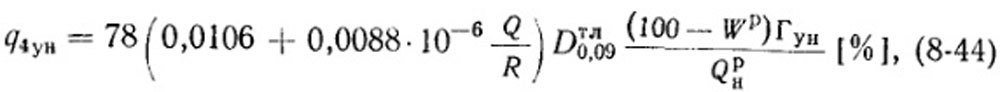
где W_р - влажность топлива, %.

На рис. 8-21 показана расчетная зависимость q_4ун от Q/R для донецкого угля марки Д при D^тл_0,09 =5% и Г_ун= 40%. В пределах Q/R=400÷1800 тыс. ккал/(м²Xч) потеря с уносом меняется от 4,5 до 8,2%.

Формулы (8-41) и (8-42) не учитывают уменьшения размеров частиц и их веса вследствие выгорания. Предполагается, что на смену уменьшившимся в размерах первоначально отвеянным частицам приходят соответственно выгоревшие более крупные частицы, находившиеся в состоянии кипения над слоем.

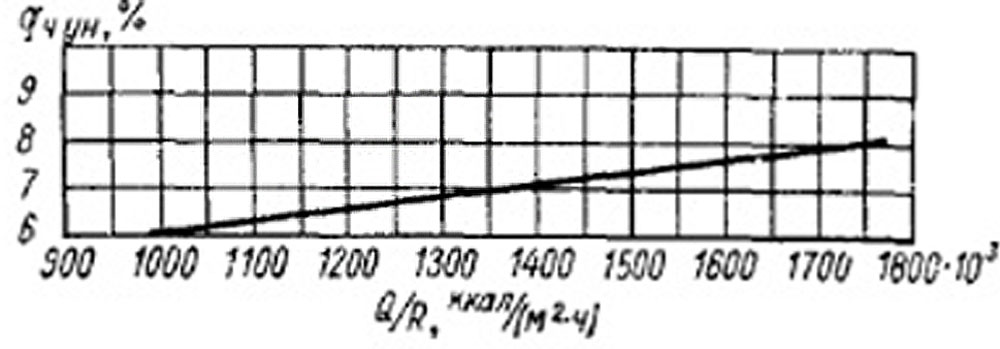
Рис. 8-21. Расчетная зависимость потери тепла с уносом от теплонапряжения решетки для топок с механическими забрасывателями.

Фактическое количество уноса может получаться увеличенным в случаях растрескивания некоторых углей в слое или выноса выгоревших частиц из слоя при небольшой зольности угля и образовании сыпучего шлака. Эти факторы пока трудно учесть. Здесь нужно вводить какие-то поправочные коэффициенты в зависимости от механической и термической прочности топлива, а также физических свойств золы последнего. Но для многих энергетических каменных и бурых углей расчеты по формулам (8-41) и (8-42) хорошо совпадают с данными опытов.

Из-за местных явлений спекания и шлакования в слое возможен обратный результат - уменьшение количества уноса, что обусловливается прилипанием мелких частиц к коксовым и шлаковым образованиям. Это отмечено в ряде опытов, когда при повышенных потерях со шлаком получились пониженные потери с уносом. Обычно шлакование слоя связано с недопустимо низкими коэффициентами избытка первичного воздуха, поэтому такие режимы работы топок следует считать ненормальными.

Существенное значение имеет конфигурация топочной камеры. Так, при испытаниях котлов энергопоезда Б-4000, СУ-9 и ДКВР-20, у которых в топках выполнены задние своды, получены увеличенные количества уноса по сравнению с тем, что имеет место при открытых камерах. Очевидно, за счет отжатия сводом газового потока к фронту и соответственно повышения скоростей газов в пережиме топки происходит отвеивание более крупных частиц топлива. Здесь мы видим результат, противоположный мнению, установившемуся на основе паровозной практики (см. § 6-5).
Выгорание уноса в топке определяется практически только одним фактором - выходом летучих топлива. Чем выше последний, тем лучше выгорает унос. Влияния других факторов, как то: теплонапряжения решетки и топочного объема, зольности топлива и избытка воздуха при промышленных испытаниях топок не замечается.

Содержание горючих в уносе для различных углей лучше всего оценивать через степень выгорания углерода кокса х_ун- характеристику, которая находится по формуле, аналогичной (8-14).

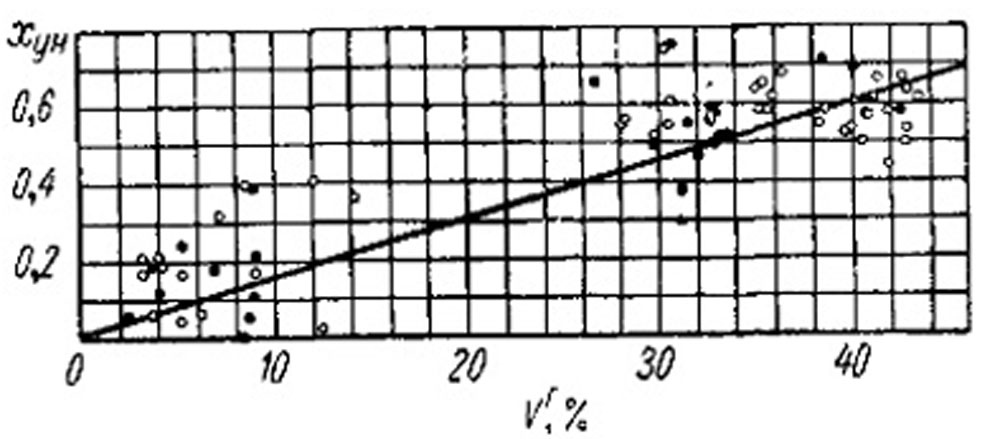
Рис. 8-22. Степень выгорания углерода кокса в уносе в зависимости от выхода летучих топлива для топок с механическими забрасывателями. • - низкие топки; ο - высокие топки.

На рис. 8-22 показана зависимость х_ун от выхода летучих топлива, построенная по данным испытаний топок с механическими забрасывателями на различных каменных и бурых углях, а также антрацитах (при отсутствии возврата уноса). Большой разброс опытных точек объясняется главным образом неравномерным распределением золы по фракциям топлива (пылевые частицы во многих случаях имеют зольность, значительно отличающуюся от средней зольности всей массы угля). По этой причине значения х_ун для тощих углей и антрацитов иногда приобретают отрицательные значения, а содержание горючих в уносе получается выше, чем в исходном топливе.
Приближенно можно принять:

где V^r - выход летучих топлива на горючую массу, %.

Выгорание уноса, вообще говоря, недостаточное. Значения х_ун на рис. 8-24 составляют для углей с большим выходом летучих (V^r=30÷45%) от 0,45 до 0,7, а для тощих углей и антрацитов (V^г=4÷13%) от 0,05 до 0,3.

Содержание горючих в уносе находится по такой же формуле, как (8-18). Значения Гун меняются для различных углей от 25 до 85%.

В табл. 8-4 приведены некоторые данные о содержании горючих в уносе по фракциям. Для частиц размером 0 - 0,09 мм оно составляет при большом выходе летучих топлива от 20 до 60%, а при малом выходе летучих от 50 до 80%. Крупные частицы размером более 0,25 мм отличаются содержанием горючих соответственно 40 - 75% и 75 - 90%. Интересно, что в уносе сохраняется небольшой процент летучих.

Таблица 8-4. Содержание горючих в уносе из топок с механическими забрасывателями по фракциям.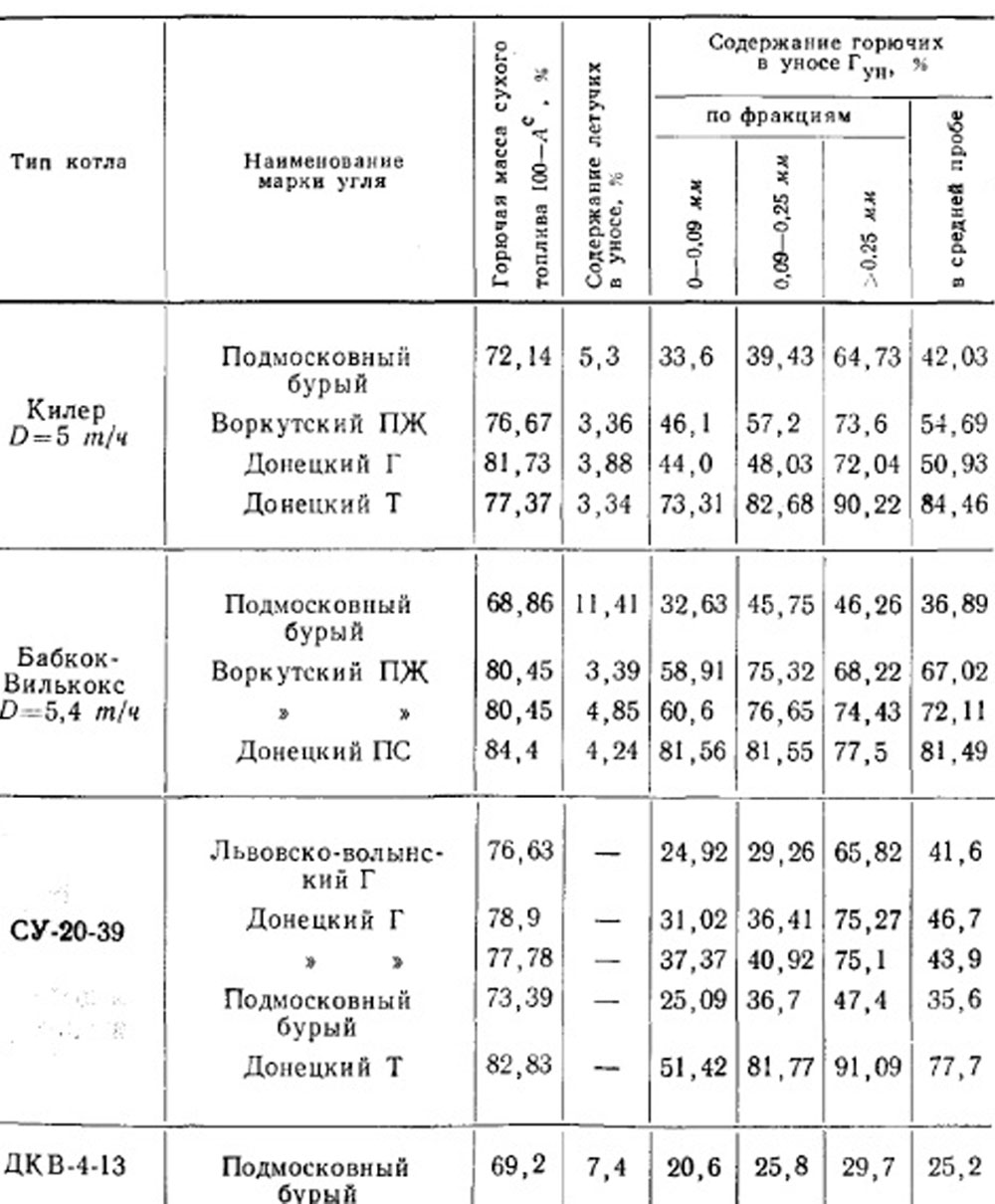

Величина х_ун иногда приобретает ложные высокие значения, если имеет место значительный дополнительный вынос выгоревших частиц из слоя. Фактически выгорание уноса не улучшается, а он просто разбавляется более озоленными частицами. При этом количество его должно быть больше расчетного.

В ряде случаев происходит дополнительное догорание осажденного уноса в зольниках или золовых бункерах котла, если там создаются подходящие температурные условия.

Давно является спорным вопрос о том, какой высоты должна быть топочная камера с точки зрения уменьшения потерь с уносом.

Анализ данных испытаний разных котлов с высокими и низкими топочными камерами показывает, что потери с уносом в тех и других случаях получаются практически одинаковыми.

Следовательно, увеличение высоты топки ничего не дает. Для точнения этого вопроса ЦКТИ были поставлены специальные исследования в отношении выгорания частиц уноса по высоте топки. Выявлено, что содержание горючих в уносе заметно уменьшается лишь до высоты порядка 2 м над слоем, т. е. в зоне достаточно высоких температур. Сказанное иллюстрируется рис. 8-23, где показаны значения Хун в разных точках по высоте и длине топочных камер котлов СУ-20 и ДКВ-10.

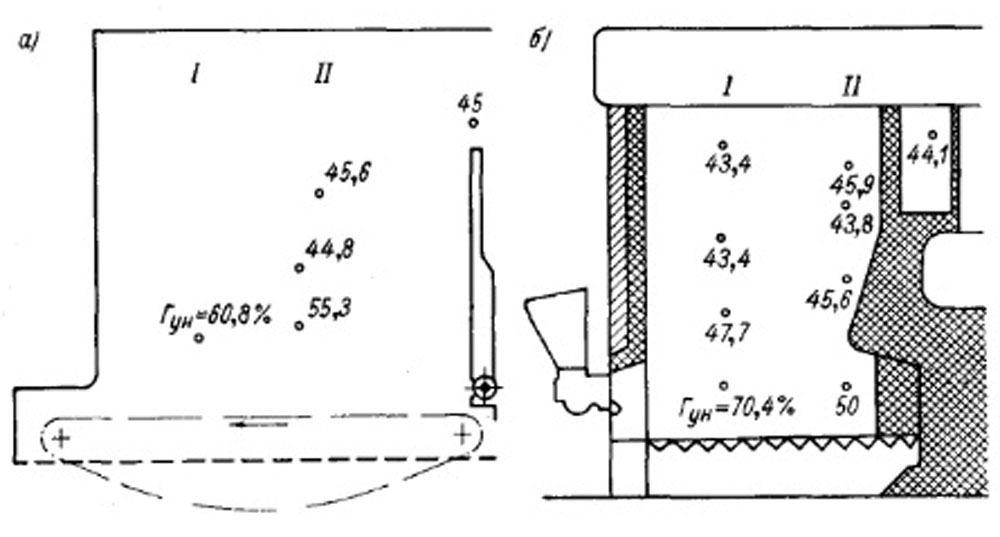
Рис. 8-23, Выгорание уноса по высоте топочной камеры: а - котел СУ-20 с топкой ПМЗ-ЛЦР; б - котел ДКВ-10 с топкой ПМЗ-РПК.

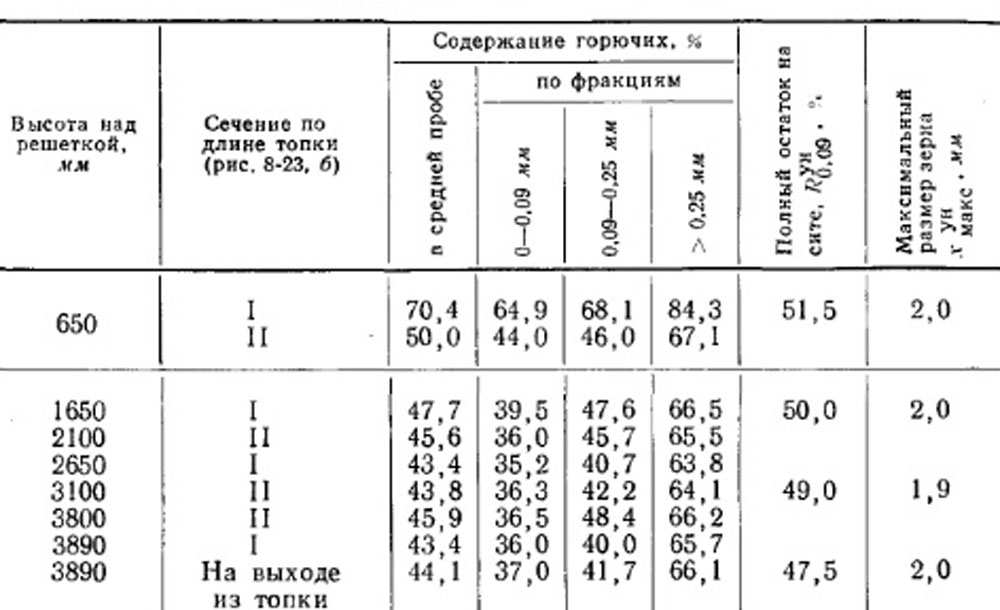
Из данных табл. 8-5 и 8-6 можно видеть, что с определенной высоты топки прекращается выгорание как крупных, так и мелких фракций.

Таблица 8-5. Характеристики уноса в разных точках по высоте и длине топочной камеры котла СУ-20.

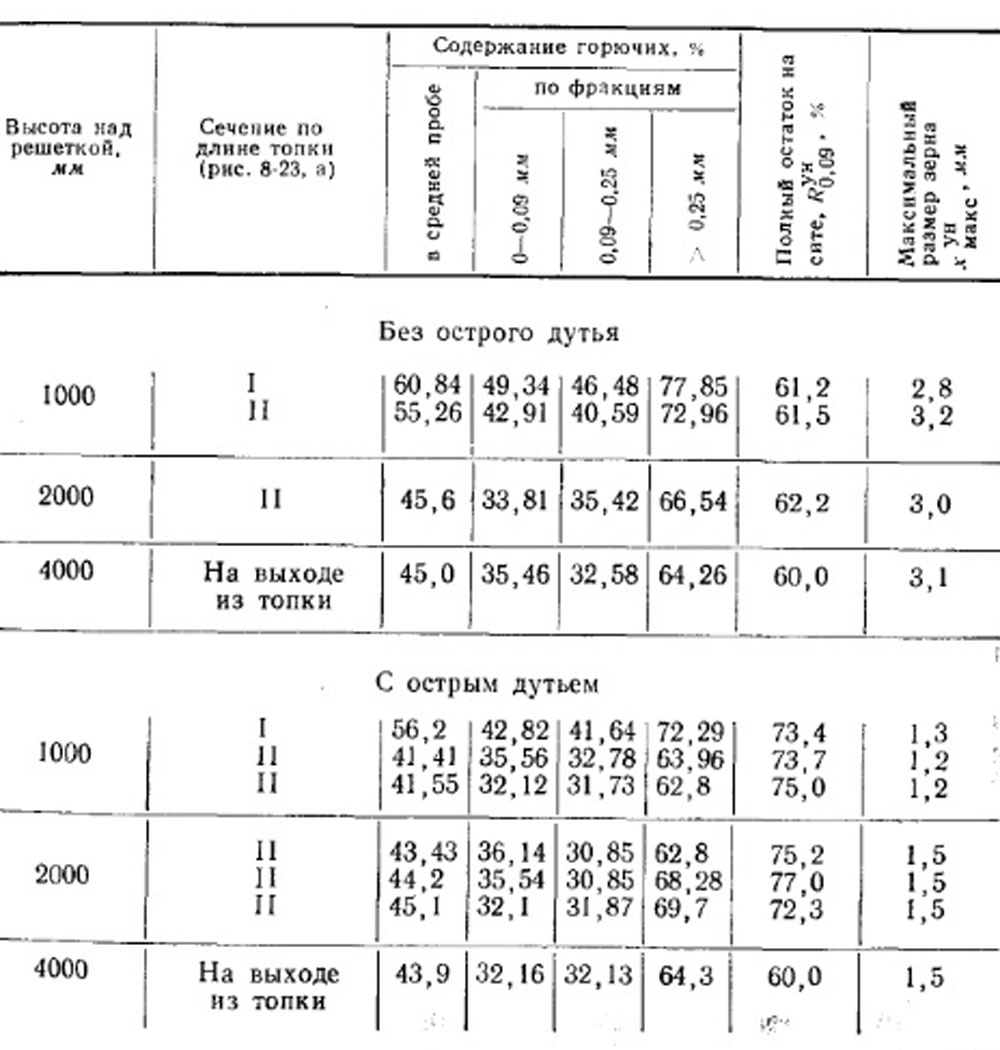
Таблица 8-6. Характеристики уноса в разных точках по высоте и длине топочной камеры котла ДКВ-10.

Характерно, что на ранее рассмотренном рис. 8-22 нельзя отметить какого-либо определенного расслоения опытных точек для низких и высоких топочных камер. Это также указывает на бесполезность большой высоты топки.

По длине топочной камеры изменение содержания горючих в уносе весьма заметно.

В принципе на выгорании уноса должен сказываться температурный фактор. Но слоевые топки работают обычно с относительно низкими температурами факела из-за сосредоточенности горения в слое, а также повышенных избытков воздуха и большой степени охлаждения топок экранами.

Для составления теплового баланса топки необходимо знать, сколько золы топлива будет переходить в шлак и сколько в унос. Доля золы в уносе определяется по формуле:

или приближенно

Концентрация уноса в газах на выходе из топки будет равна: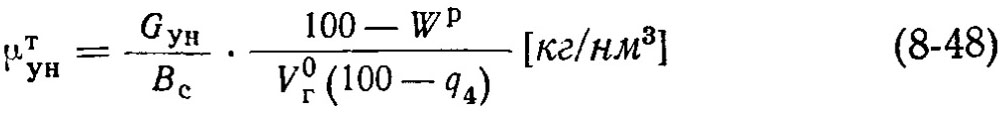  

Или приближенно

При анализе данных испытаний топок с механическими забрасывателями рекомендуется пересчитывать значения G_ун/B_c и q_4ун на одно какое-нибудь содержание пылевых частиц в топливе (D^тл_0,09=5 или 2,5%) по формулам:

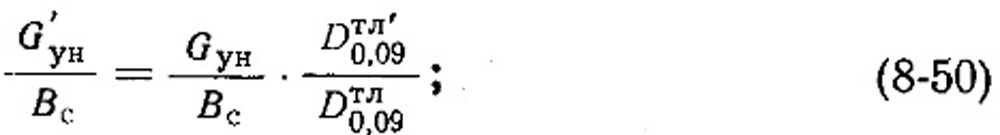
Установленные закономерности в отношении уноса, очевидно, будут справедливы и для топок с пневматическим и паровым забросом топлива. Однако в случаях топочных устройств с низконапорным пневмозабросом и цепной решеткой прямого хода, возможно, придется вводить поправки на неравномерность скоростей газового потока над решеткой. Применимость выведенных формул к другим слоевым топкам пока не ясна.